Double-Ended Chess

By Peter Aronson

Introduction

     Double-Ended Chess is a variant of Chess where captures are by withdrawal and approach, as in the Malagasy game of Fanorona. However, unlike in Fanorona, individual pieces are captured, not lines, and captures can be made both by withdrawal and approach in the same move. The setup and play is generally like orthodox chess, but the Queen's Knight is replaced by a Mirror-Knight, that moves like the regular Knight, but captures differently.

Board and Setup

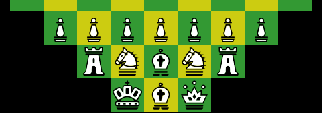
     The setup is identical to that of orthodox chess, except that the Queen's-side Knight is replaced by a Mirror Knight, represented by an upside-down Knight in the graphics.

General Rules

     The rules of Double-Ended Chess are identical to those of orthodox chess, except when noted otherwise. Capture is completely different, as described below, but movement is standard, including Pawn double-move and Castling. Check and mate work as usual, allowing for the difference in capturing method.

Capturing

     Capturing is by withdrawal and by approach instead of orthodox chess's usual method of capture by replacement. It is never possible in Double-Ended Chess to move into an occupied square. Both capture by approach and capture by withdrawal can occur as the result of a single move.

     Capture by withdrawal occurs when a piece is adjacent to an opposing piece, and moves away from it in the same line.

     Capture by approach occurs when a piece is moved next to an opposing piece in the same line as the movement.

     In the diagram below, the white Queen moves from its starting position in the lower-left to a new position in the upper-right. If an opposing piece was on the square marked with a red circle, it would be captured by approach. If an opposing piece was on the square marked with a green circle, it would be captured by withdrawal.

     While moving to capture is not obligatory (except as under the normal rules of orthodox chess, such as relieving check), when moving in Double-Ended Chess, any captures by approach or withdrawal occur automatically; if you withdraw from, or approach an opposing piece, capture occurs. You can not move away from, or move to an opposing piece, and not capture it if the movement is in line with the piece.

     Pawns may move diagonally only to capture, and then only forward, but such captures can be by approach, withdrawal or both, so a pawn can either capture a piece that is two squares diagonally ahead of it, or immediately diagonally behind. There is no special en-passant capture, but if the appropriate square is empty, it is possible to capture a Pawn that has just double-moved as if capturing en-passant by a normal capture by withdrawal.

     Knights are considered to move a single square orthogonally, possibly jumping over a friendly or opposing piece, then a single square diagonally outward (the withdrawal capture occurs in the orthogonal direction, the approach capture in the diagonal direction). In the diagram below, the white Knight moves from its starting position in the lower-left to a new position in the upper-right. If an opposing piece was on the square marked with a red circle, it would be captured by approach. If an opposing piece was on the square marked with a green circle, it would be captured by withdrawal.

     Mirror-Knights move like Knights, but in the opposite order: a diagonal move followed by an orthogonal move outward (the withdrawal capture occurs in the diagonal direction and the approach capture in the orthogonal direction). In the diagram below, the white Mirror-Knight moves from its starting position in the lower-left to a new position in the upper-right. If an opposing piece was on the square marked with a red circle, it would be captured by approach. If an opposing piece was on the square marked with a green circle, it would be captured by withdrawal.

     The King does not capture by withdrawal when castling, even if an opposing piece is adjacent to it.

Subvariants

     Deep-Capturing Knights. In this version, there is only one kind of Knight, and it treats its move as a single, atomic movement. Thus, the square attacked by withdrawal is a duplicate Knight's-move behind the Knight's starting square, and the square attacked by approach is a duplicate Knight's move ahead of the Knight's ending square. In the diagram below, the white Knight moves from its starting position in the lower-left to a new position in the upper-right. If an opposing piece was on the square marked with a red circle, it would be captured by approach. If an opposing piece was on the square marked with a green circle, it would be captured by withdrawal.

Notes

     Doubled-Ended Chess was inspired by the unique methods of capture used in the Malagasy board game of Fanorona. In particular, it was inspired by a Malagasy saying:

“It is unfair to bite at both ends simultaneously like a leech.”

     This game is sort of a companion piece to my game Jumping Chess, in that both of them use pretty much the standard orthodox chess setup, but different means of capturing. I've always found Fanorona's means of capturing fascinating, and it was fun to try them out in a Chess context. Of course, capture by withdrawal has already been used in Abbott's game of Ultima, but I've never seen a Chess Variant that uses capture by approach. I combined the two, and made them automatic, as opposed to letting the moving player decide to use one or the other or even neither, as I felt that this made the consequences of a move clearer, and that clarity in a game was important. As a result, sometimes a piece can be indirectly pinned, as moving it would capture an opposing piece who's removal would cause check.

Zillions of Games

• double-ended.zrf