Immortal Chess
This game deserves a bigger board but I wanted to keep it simple. I am not sure if anybody has ever tried before to use chess pieces with hidden identities. I came up with this idea a while ago, and I realised that this could be a great addition to the game of chess.
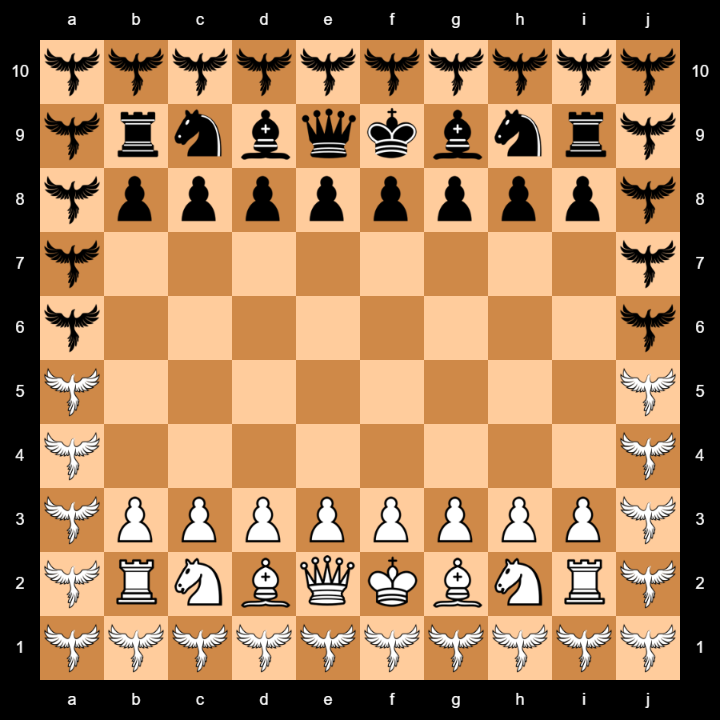
Setup
The initial setup looks like this:

Pieces
Each player has a complete chess set of 16 pieces. Pawns promote on the last rank of the 8x8 central board.
Both players share 36 Immortals that are placed around the border.
Immortals are neutral pieces and can be moved by both players. Immortals have hidden identities. They enter the game through a non capturing Queen like move, then get flipped over and replaced by the piece they represent. This counts as a single move.
Army composition of the Immortals
Each player has 18 pieces hidden as Immortals:
- 7 Knights
- 5 Bishops
- 4 Rooks
- 2 Queens
Immortals cannot be captured in their initial position. Since they are neutral pieces (until they get flipped over) Kings are not in check while in their range.
While bringing them into the game players have to make sure that they are moved at a safe distance from their own King, so that their own King might not be in check.
Rules
Each player has two moves per turn:
- A regular chess move
- Bringing an Immortal into the game
The moves are played in this order.
The entire board is available for the game but regular pieces cannot move into border squares occupied by Immortals. Also, Immortals cannot move along the border. They are only allowed one Queen move towards the centre of the board.
Players may skip the second move if they wish so.
Notes
An alternate version of this game makes the Immortals non neutral, but they have to be placed in their own half of the board.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Florin Lupusoru.
Last revised by Florin Lupusoru.
Web page created: 2024-03-17. Web page last updated: 2024-03-17
