MonadChess

Below are shown new setup for Azchess without above mentioned blank and in addition, knights are located more close to the center and piece set is complete with all combinations of the moves of the light pieces Knight, Bishop and Rook, each Pawn was covered, three consistently located squares has been differently filled. And also in this game has been used most popular the East Chess pieces - the Cannon and the General (or Amazon). In this sketch our basic purpose was designing maximum symmetric game.

It is an abstract and a symmetric wargame with no random chance.

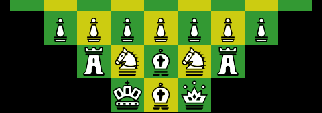
Figure 1, Monadchess.

Setup

Black: 3pppp3 / pppp2pppp / rnb1g2bnr / 2oqkcao2

Pawns protection: 1124X X4211 ,

Pieces density =50% exactly as for Orthodox Chess. Free squares on the first, second and third row are equal 4,3 and 2.

Quantity Pawns = 12 ; Ouantity Pieces (without a King, it is special Piece and located special square of the Chess game - on the "golden section" of horizontal line = 0.618) = 12.

In this setup most Chess parameters are equal and symmetric. The midpoint of Central symmetry is located between squares e5, f5 and e6, f6. The Basic condition of Chess games is: "contenders should have equal opportunities before game" and this is fulfiled. "Mirror Image" moves for Black are not possible. For example: 1.f3-f5 e8-e6, 2. f5-e6 .... Symmetry is destroyed.

"The perfect symmetry is required to completely minimize the starting advantage of White" - Derek Nall. For example:

1.White squares = Black squares;

2.Identical pieces from both sites;

3.Identical setup -The start position for both Army (or "Forces of Order") is absolutely symmetrical from the point of view of mathematics. All double Pieces are located on the squares of same color. The midpoint of the revolving symmetry is located between squares e5, f5 and e6, f6.;

4.Symmetrical pawns protection (Horizontal and Vertical lines);

5.Free squares (on the begginig of the game) = Squares with pieces (Pieces density =50%);

6.Identical Chess rules for both sites ( both sites are using identical Pieces);

7.Shape of the board is square (not rectangular). The square board has advantage above rectangular one (for example, 10x8; 14x8 and so on), because the square board has the central symmetry to an average point of a board but rectangular has not and also the rectangular board sharply reduces influence of pieces in comparison with a square board;

8.The Pawns quantity equal to the Pieces quantity;

9.The diagonal force lines on the board are symmetrical;

10.All of orthogonal forces lines are well balanced;

11.Quantity of Pieces with simple moves (Knight,Bishop,Rook,Cannon) = Quantity of Pieces with complex moves (Archbishop,Chancellor,Queen,General);

12.The Opening setup is a Centrally symmetric* (not "mirror image") The Principle of Transition applied in a Chess.;

13. Pieces with simple moves are pair and Pieces with complex moves are not, a like Orthodox Chess;

14.The Board is 10x10 and quantity different Pieces is equal to 10, too;

Therefore the name of the game is Monadchess**.

Pieces

A-Archbishop - has the combined moves of a Bishop and a Knight, (B+N); C-Chancellor - has the combined moves of a Rook and a Knight, (R+N); G-General - has the combined moves of a Queen and a Knight, (Q+N); Q-Queen - has the combined moves a Bishop and a Rook, (B+R).

O-Cannon moves to capture as an Orthodox Rook which is required to hop over a single screen. In other words, O - capture by hoping over a second piece in order to capture a third piece. For example, O - on a1 can take a piece on f1 when exactly one of the points b1, c1, d1, or e1 is occupied by a piece of either color. O - only capture when hoping and only hop when capturing. They may never hop over more than one piece in a given move. O - needs an intermediate piece between itself and its victim. O - jumps the intermediate and take the victim on its square. The intermediate is left unaffected.

Rules

Notes

G = Q + N > Q = R + B > C = R + N > A = B + N > R > O > B > N >; and approximately G = (12 - 14)P; N = (2.5 - 3)P.

A P P E N D I X

Below, graphic representations of used pieces are shown:

- General; - Queen; - King; - Bishop; - Cannon; - Knight; - Chancellor; - Archbishop; - Rook; - Pawn;

*- Very good illustration of the Central symmetry for Monadchess, emphasizing an arrangement of the Kings on a board.

**-

The famous Chinese Monad - Either side of the two opposites always restricts and acts on the other (f.exp. quantity Vs quality, White Vs Black and so on). This process of mutual restriction and interaction is the operation of yin and yang, without which change would not occur. Thus the two opposites of yin and yang do not exist as an entity in a still and unconcerned state. They constantly interact with each other, hence the alteration and development of an object. Each of the two aspects is the condition for the other's existence and neither can exist in isolation. For example, daytime is yang, night in yin, without day there would be no night; upper is yang, lower is yin; left is yang, right is yin, etc., each pair exists in a state of mutual dependence, and without its opposite it could not exist. In certain circumstances and at a certain stage of development, each of the two aspects of yin and yang, within an object, will transform from yin into yang and from yang into yin. The mutual consuming-increasing of yin and yang is a process of quantitative change, and the mutual transformation of yin and yang is a process of qualitative change. The above-mentioned relationships of mutual opposing, depending, consuming-increasing, and transforming of yin and yang are the basic content of Yin-Yang theory. (Yin = Yang) it is perfect balanced situation.

Example 1 (Quantity Vs Quality): The quantity and quality in turn are contrasts. Quality, accrueing up to a maximum, gives rise to quantity. The quantity gives rise to quality. Especially well it is visible on an example "Queen`s gambit" in a Orthodox Chess. The Queen, the most valuable Piece on a chessboard is endowed. Owing to it item advantage which conducts to a victory is reached. Quality turns to quantity. The situation becomes equivalent to quantitative overweight of pieces(for short time).

Example 2 (Attack Vs Defence): When attacking do not forget about defence. "The martial art Tai Chi Chuan, has a number of ways imbedded in its forms. It is a deceptively effective martial art to extent that many of the peaple practicing its forms do not even realize it can be used for self defense. The forms are practiced in a very slow dance-like manner with graceful movements with flowery names, such as "play the lute". If an opponent steps toward a adversary and foolishly throws a punch at the opponent`s stomach, the opponent can counter with "play the lute". In this move the opponent would simultaneusly trap the agressor`s closest knee. To protect his knee the agressor must move backward but this tightens the joint lock. to release the join lock he must move forward but this makes his knee vulnerable. In short, the agressor is going to lose no matter what he does". - Intuitor Chess Strategy.

For this reason it has been decided to balance in the given game of force of protection and attack by increasing quantity of Pawns. Monadchess is final result of the essays: Yin-Yang Principle and Chess, and Optimum design Chess variant.

Example 3: (Pieces not equal to Pawns) Let`s consider two extra variants initial position (Pieces density 60%) where Pawns > Pieces I variant (White) and Pieces > Pawns (Black) II variant.

Figure 2 The 2 variants are shown together in one picture.

In I variant games goes basically between Pawns.

In II variant games goes basically between Pieces.

And any way, Super Symmetric Setup (Figure 1) where Pieces = Pawns and Pieces density is equal 50%, is most aesthetic and optimum variant from symmetric point of view. And in addition playable from practical point of view, too.

In the games "Super Maharadscha" or "The Invisible Man" opening setup for the side playing against The Maharadscha or The Invisible Man must be good protected. In the Figure 3 are shown opening setup for Monadchess where is all Pieces mutually protected.

Figure 3, All Pieces Mutually Protected.

P.S. In "Gustavian Cannonrider Chess" You can find new Chess Piece "Cannonrider" (invented by Mats Winther). This Peace is very interesting and difficuld for calculation. And I think for Chess players it will be useful to use Cannonrider in own games.

On black squares Cannonriders move like Rooks, by sliding any number of squares along a row or column, but they can capture an enemy only if there is a piece (of either side) in between. Thus to capture they leap over the intervening piece and land on the enemy piece, like a cannonball. If positioned on a white square it jumps like a nightrider, that is, can make continuous knight jumps in the same direction, provided that the interim squares are empty.

I think if we will use this Piece in Monadchess or will change Amazon for Cannonrider then we will have SSS Chess (Super Symmetrc Setup).

White: 3PPPP3 / PPPP2PPPP / RNB2G1BNR / 2O(Cr)CKQO2

Black: 3pppp3 / pppp2pppp / rnb1g2bnr / 2oqkc(cr)o2

Cr - Cannonrider.