Chess on a Tesseract
Way back in the 1970s, while I was playing the 3D variant called Strato Chess, I started to wonder (as others here have done) if the dimensions of the game couldn't be extended to four or even five. It took some time to figure out, so I set the idea aside.
Eventually, upon learning about such figures as the tesseract and penteract, I started to think about how we three-dimensional beings would interact with such things. I even started writing a story about a group of people trapped in a structure built around a pentaract (with similar effects to what I'm about to describe).
It was only relatively recently that I managed to put the two ideas together. The play is, at one level of thought, as two-dimensional as orthodox chess; but on another level, it still uses four dimensions of movement.
The Geometric Concept
This game is played, ostensibly, on the two-dimensional "faces" of a tesseract. To help understand how that works, let's subtract one dimension, and consider the edges of a cube.
Suppose this game were to be played in such a way (and I wouldn't put it past the contributors of this site to come up with one). When a piece reaches a corner, there are two other edges that it continue onto. How does one choose which to go to?
The principle is the same here. Each edge of a face meets an edge of two other faces; when a piece goes off the edge of a face, the player chooses which of the two connecting faces it goes to.
To help players keep track, each face has a two-digit coordinate code to indicate show where it is. Each digit is from 0 to 7, and each code is written with the smaller digit first. No combination of two digits appears twice.
The initial codes have two main cubes, parallel with one another, with their faces numbered 1-6 like a game die so that opposite sides add up to 7. The cube for White adds a leading 0, while the cube for Black adds a trailing 7. All other Faces are numbered according to the two faces they connect to; for example, Face 35 is between faces 3 and 5 on both cubes, connecting with 03 and 05 on one end and 37 and 57 on the other, then with 13 and 15 on one side and 36 and 56 on the other.
The challenge is showing this, of course, is that tesseracts are very difficult to illustrate in the two dimensions of a computer screen (or a sheet of paper) -- much more so than cubes. There's so much to a tesseract that any two-dimensional illustration of the entire thing, including a label for each side, becomes so busy that it's hard to read. (If cubes could be trained like dogs, tesseracts would be cats.) Despite this, these illustrations should give at least a general idea of how this works.
In the classic cube-within-a-cube projection of a tesseract (called a Schlegel diagram), the playspace would look something like this:
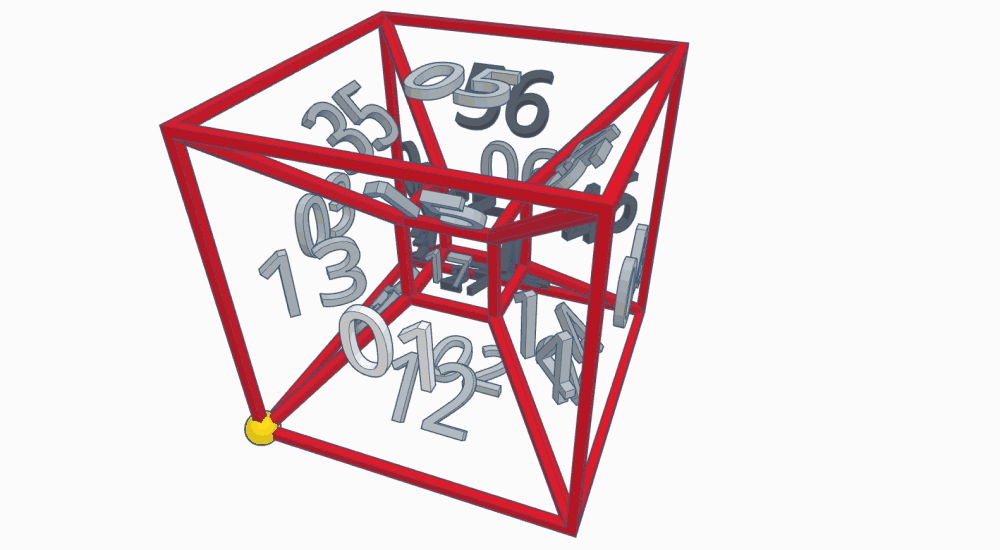
As noted above, the complexity of the tesseract makes it a bit hard to read; you can get a general idea from this, but it's rather dense.
It may help a little to look at it one part at a time. Here's a diagram of just the faces that will be White's for this game:

That, at least, is a considerable improvement. Now, the same for Black:

That's just as hard to read as the first diagram, mainly because of the size of the "inner" cube, though the parts that are legible can help to extrapolate the obscured numbers.
The six Faces that are neither White nor Black are considered Grey:

That's almost as good as the White illustration, above.
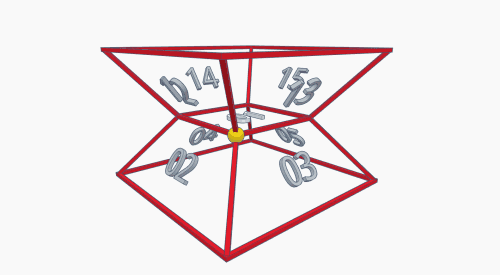
As an alternative, let's take a general look at a tesseract in a "side-view" projection:

This shows two cubes, one white and one black, overlapping and connected at their corners by eight bars of equal length to the cubes' sides. Take a face of one cube, the corresponding face on the other, and the four bars that connect them, and you havwe another cube in the tesseract.
These two illustrations (clicking on either will bring the picture up full-size in a new window) show how the faces for this game are arranged on the tesseract.
It's a considerable improvement as far as legibility, but still a little hard to read. Nonetheless, recognizing the patterns can help. Note, for example, how Face 14 (at the right in the first illo) is opposite Face 36; the first digit of each number and the last of the other adds up to 7, so you know they're complementary. Also, each digit has six sides that all form one of the tesseract's eight cubes; 0 and 7 are plain to see, but you should also be able to make out (on either this projection, or the Schlegel diagram above) how the faces for at least Cube 4 and cube 5 are arranged.
The next two illustrations show, from a completely different perspective, only the Faces where White and Black set up.
As indicated above, a piece leaving Face 01 in the direction shown as down and left in the above illustration would have a choice of going to Face 02 or Face 12. Similarly, a piece leaving Face 37 in an upward direction (as seen in the second illustration) could choose to go to either Face 67 or Face 36.
On the first illustration, the yellow sphere represents where, as the juncture of 1, 2, and 3, all notation begins (see below).
Here's what these two look like together, with the Opposing Faces also shown:

Face 06 is at both the top and the bottom, because this is actually a loop around the tesseract; it could go on forever.
Hopefully all this gives a reasonably clear view of how the tesseract's Faces relate to one another in this game.
Setup
Boards
The 24 Faces of the tesseract are each made up of a 5x5 board. The corner spots of each board are blacked or whited out; no piece may enter or pass through them. Wherever two Faces meet, the black and white spaces must match up. (This isn't generally possible to do in a literal sense, but they should be treated that way when moving from board to board.)
In a physical game, the boards can be laid out however you wish, though a recommended layout is presented below. Each should have an indicator as to which Face it represents, and a guide on each edge as to which two Faces it leads to.
Pieces
In the figure above, White sets up on and around Face 01, while Black sets up on and around Face 67. The setup is essentially identical for both, so only White is illustrated.
On each Home Face, the King goes in the center. Orthogonally adjacent, he's flanked by two Nightriders; each has a Queen clockwise from it, and a Bishop counterclockwise. The remaining two spaces next to the King are filled by an Archbishop and a Chancellor. The outer spaces, going around from the corner next to each Bishop, are filled by a Rook, Knight, Bishop, Archer, Knight, and another Rook.
These may be rotated however the player prefers, including reversing direction (for a total of 8 possible setups). Black and White need not set up identically, or even consult with each other at all, unless they want to.
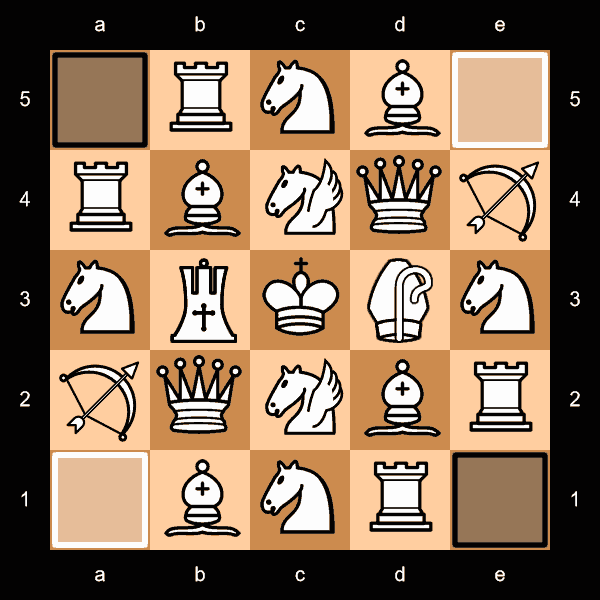
Adjacent to each side of the Home Face are two more Faces; these eight are the Territory Faces. On the edge of the Face adjacent to the Home Face, each player has a Berolina Spear, flanked by two Arabian Spears. The next row over has three Standard Pawns, one in the center and one at each end, with Berolina Pawns filling the other two spaces.

(This is just a generic illustration; the actual Ranks and Files, including the orientation, will be different for each Face.)
Physical Setup
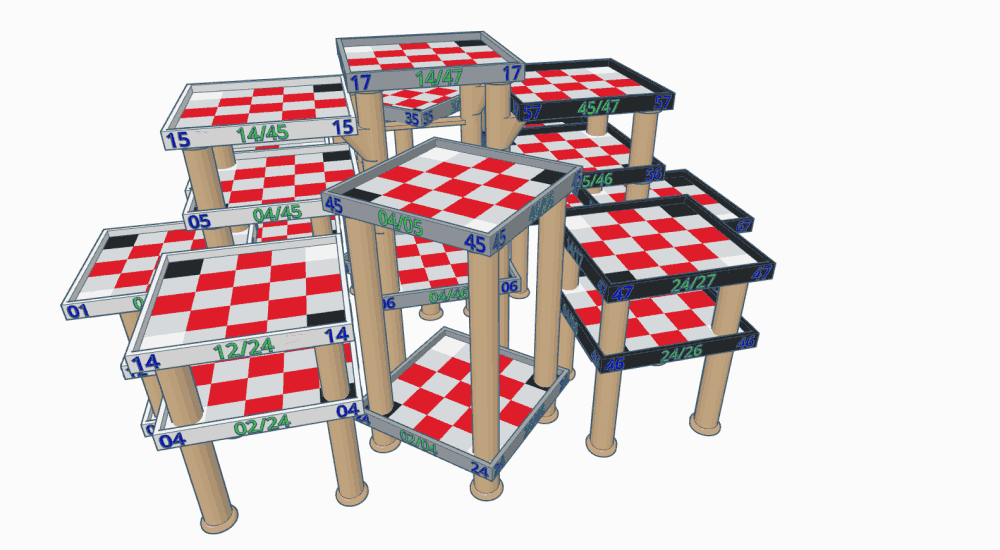
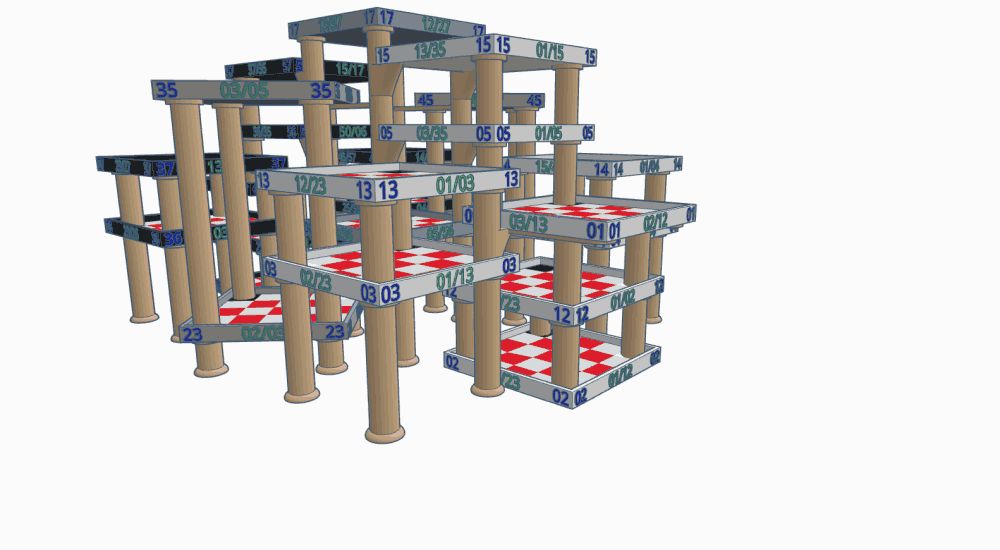
While this may seem overwhelming, it's quite possible to set this game up for a face-to-face contest. It would all but require a large 3D setup, however -- though with lots of table space a 2D arrangement is possible.
The illustrations below show what a 3D setup for this game might look like. (Right now it's just hypothetical, but if I ever get to build it I'll make a separate page for it.) All of these illustrations are clickable to show a full-size version in a new browser tab.
If built for the 2" squares that are considered standard in chess circles, this structure would be just a tad under 4' long, 3' wide, and 2' high. That's huge as 3D chess structures go, but modest when you consider that it's host to 24 5x5 boards in a non-linear array. Still, not all dinner tables measure 3'x4', so it may be necessary to reduce the squares to 1.5", making the structure 3' long, 2'3" wide, and 1'6" high. The gap between levels and between posts (which is important for reaching pieces on lower-level Faces, especially 06) is 5" on the full-sized version, or 3.75" if reduced.
I envision this with the squares printed on cardstock, the trays either 3D printed or made from cardboard, the labels printed on sticky labels, and the legs (and accessories) made from wooden dowels, PVC pipe, or something similar.
Pieces
Each player is equipped with the following:
- 1 King
- 1 Archbishop
- 1 Chancellor
- 2 Queens
- 2 Nightriders
- 2 Archers
- 4 Bishops
- 4 Knights
- 4 Rooks
- 8 Berolina Spears
- 16 Arabian Spears
- 16 Berolina Pawns
- 24 Standard pawns
The pieces with links are either orthodox Chess pieces, or pieces familiar to most chess variant aficionados; the articles explain the moves. The other three pieces:
Archer: Moves two spaces diagonally, or "rifle-captures" (captures without moving) a Knight's move away.
Arabian Spear: A sort of "Pawnrider," moves without capture directly forward like a Rook, or captures forward like a Bishop.
Berolina Spear: Moves without capture forward diagonally like a Bishop, or captures directly forward like a Rook.
Pawn/Spear Movement
For Pawns and Spears, moving forward means whatever direction takes the piece closer to the opponent's Home Face. This means that the Spears will infrequently, and the Pawns almost never, move to any of the Open Faces or Opposing Faces; the shorter route from any Territory Face (where the Pawns and Spears start) to the opponent's Home Face always is always through an opponent's Territory Face. Where there's a choice between going to an Open Face or the enemy's Territory Face, or between the player's Territory Face or an Open Face, choosing the latter (in each pair) is mandatory.
Should a Pawn or Spear go to an Open Space, the closer direction is toward the nearest edge that leads to an opponent's Territory Face. If two (or more) are equidistant, the player may choose which way is forward.
On an Opposing Face (06 and 17), all directions are equal; Pawns and Spears suddenly have four-directional movement on these Faces, until they leave.
Rules
As noted above, when a piece reaches the edge of a Face, the player chooses which of two neighboring Faces it continues to. The move is as seamless as if the boards for the two Faces were set against one another.
The board setup makes Castling impractical, if not impossible. However, en passant is used with the Pawns (Standard and Berolina), though not the Spears.
In terms of the endgame (checkmate, stalemate, etc.), all standard rules are observed.
Both types of Pawn and both types of Spear promote upon entering the opponent's Home Face. They may promote to any type of piece that's used in the game, except of course for the King and other Pawns or Spears.
Notation
As noted above, the corner where 1, 2, and 3 meet (Faces 01, 02, 03, 12, 13, and 23) is the "zero point," where notation starts. Ranks (starting with 1) begin along the border between 1 and 3, while Files (starting with a) begin along the border between 1 and 3. These letters and numbers go in both directions, so that all six faces starting at that zero point have squares a1 adjacent to that point.
The tesseract's geometry will lead to apparent conflicts as to how some of the faces should proceed. For example, leading off Face 01, Face 05 continues the Files from f-j, while Face 04 continues the Ranks from 6-10. But these two also share a side with Face 45. How should that Face proceed? In a case such as this, precedence goes to the Face with the lower number; thus, each Face is a continuation of the lowest-numbered Face that's adjacent to it. In this case, 45 would start with f6 in either event, but would follow Face 04 to match its Ranks.
 Following this method, the highest space designation would theoretically be t20. In practice, nothing ever goes beyond e15, j10, or o5 (and even those are mainly on Faces spawning from Face 01)..
Following this method, the highest space designation would theoretically be t20. In practice, nothing ever goes beyond e15, j10, or o5 (and even those are mainly on Faces spawning from Face 01)..
The notation for a specific space can then be given as the ID for the Face, a colon, and then the rank-and-file designator for the square. For example, the White King starts on 01:c3, while the Black King starts on 67:c13.
Of course, this also means that the Ranks of one Face will run into Files of another. That's OK; just go with it. It may seem confusing at first, but the goal in this case is to give each square a unique identifier.
The illustrations here should give an "official" sense of how this would go.
Where two Face numbers appear with a slash between, that means that both of those two Faces follow the pattern from the main one. Two adjacent faces with double numbers are a continuation; the first Face in each pair connects to the other, and the same with the second Face.
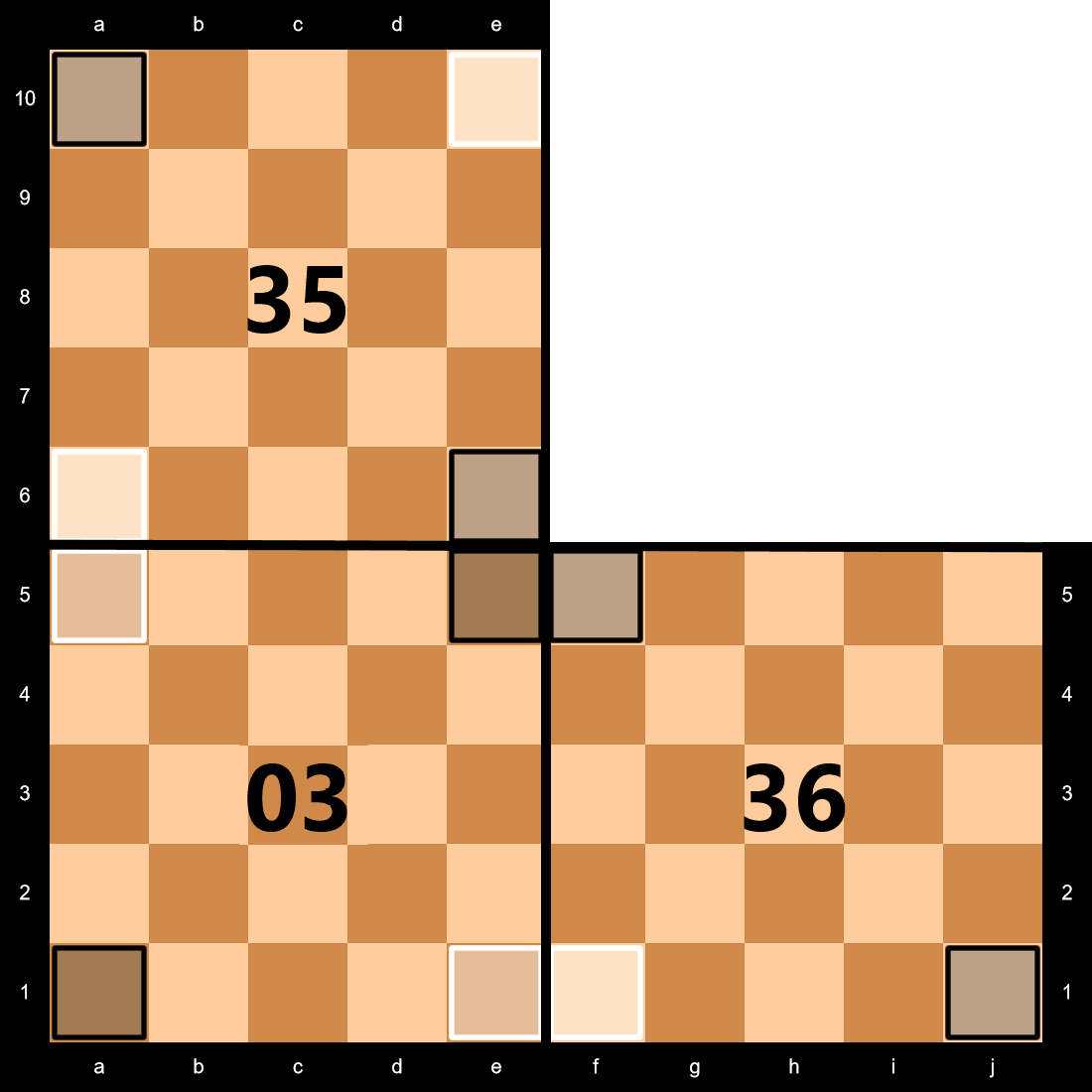
 Note that, in the first illustration (for Face 01), Face 45 takes its numbering from Face 04 (the lowest-numbered adjacent Face). Faces 05, 14, and 15 can still move there, of course; this only affects the rank/file designations. (The red line only separates the numbering, not piece movement.)
Note that, in the first illustration (for Face 01), Face 45 takes its numbering from Face 04 (the lowest-numbered adjacent Face). Faces 05, 14, and 15 can still move there, of course; this only affects the rank/file designations. (The red line only separates the numbering, not piece movement.)
You may also notice that a couple of Faces (56 and 67) appear on more than one chart. This is simply because those Faces just happen to follow the same numbering even if followed from the later directions. The numbering still comes from the lowest-numbered Face; the matching is just a mathematical coincidence.



 As for the orientation of the board on the tesseract, Face 01 sets the standard, with the ranks (numbers) along the edge with 03 and 13, and the files (letters) along the edge with 02 and 12. Those four Faces keep pace with 01, while Face 23 shares its ranks with 02 (though that's admittedly less important, since no other Face continues Face 23's count). The illustration here gives a Schlegel's view of the starting corner; the green arrows are positioned at a1 (a black blockout square), and point in the direction that the Rank numbers increase.
As for the orientation of the board on the tesseract, Face 01 sets the standard, with the ranks (numbers) along the edge with 03 and 13, and the files (letters) along the edge with 02 and 12. Those four Faces keep pace with 01, while Face 23 shares its ranks with 02 (though that's admittedly less important, since no other Face continues Face 23's count). The illustration here gives a Schlegel's view of the starting corner; the green arrows are positioned at a1 (a black blockout square), and point in the direction that the Rank numbers increase.
Notes
As a person on the autistic spectrum, one of the "plusses" I experience is the (generally useless) ability to, with some effiort, visualize four-dimensional space (or, with much effort and if the geometry is simple, even five; six is beyond me). Thus, I can visualize the actual tesseract in this game, while most if not all other people could not.
This was initially presented not so much as an actual, playable game, but as an exercise to help others visualize and understand higher spatial dimensions. As I've developed the game (with much help from Fergus Duniho and others), I found that a practical playspace would be very possible, and might even be easier to play on than a computer setup. The structure mentioned here is the theoretical version of that, but I hope to give it an actual try before long.
The Future
This may be the first chess game to take place on the surface of a tesseract, but I hope it isn't the last. There are many possiblities for further variations, with different Face sizes, different pieces, and so forth. It wouldn't even surprise me if another creator can explain the tesseract's surface better than I have here.
About That Story
The short story I mentioned in the Introduction got started, and I knew the ending as well as most of the plot points but never actually completed it past Page 2. It really was a story meant to explore the concept of moving around the three-dimensional aspects of five-dimensional space in the same way that this game explores two-dimensional aspects of four-dimensional space; one added feature was that, depending on the route one took, one could re-enter a room with "up" in a different direction than when one left, leading to some rather Escher-esque moments.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Bob Greenwade.
Last revised by Bob Greenwade.
Web page created: 2023-09-12. Web page last updated: 2023-12-16