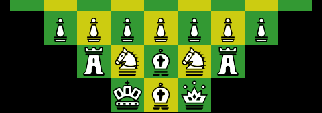
Lynx Chess
Lynx is a piece once appeared in one fairy chess problem by Colin Richard Flood. It's a compound of Rook+Knight+Zebra.Setup
files=12
ranks=12
promoZone=1
promoChoice=BGCSLT
graphicsDir=/graphics.dir/alfaeriePNG/
squareSize=50
graphicsType=png
royal=K
firstRank=1
borders=0
coordColor=#ceb5a1
lightShade=#b59378
darkShade=#7d6c62
rimColor=#423930
pawn:P:ifmnDfmWfceF:pawn:a4,b4,c4,d4,e4,f4,g4,h4,i4,j4,k4,l4,,a9,b9,c9,d9,e9,f9,g9,h9,i9,j9,k9,l9
bishop:B:B:bishop:e1,h1,,e12,h12
Gingaroo:G:FXA:giraffe:d1,i1,,d12,i12
camelrider:C:CC:camelrider:b1,k1,,b12,k12
bentshaman:S:AFmpafaFampafF:bentshaman:c1,j1,,c12,j12
Lynx:L:JRN:chancellor2:f1,,f12
Buzzard:T:GmpafmpafyafsF:/graphics.dir/alfaerie-fpd/%firebird.gif:a1,l1,,a12,l12
king:K:KisO4:king:g1,,g12
White:
Pawn a4-l4; Buzzard a1, l1; Camelrider b1, k1; Bent Shaman c1, j1; Gingaroo d1, i1; Bishop e1, h1; Lynx f1, King g1
Black:
Pawn a9-l9; Buzzard a12, l12; Camelrider b12, k12; Bent Shaman c12, j1; Gingaroo d12, i12; Bishop e12, h12; Lynx f12, King g12
Pieces
 | Pawn | Slides to the 2nd square straight ahead to an empty square if it has not moved yet, steps one square straight ahead to an empty square, or diagonally forward for (e.p.?) capturing only |
 | King | Steps one square in all 8 directions, or castles by stepping 4 squares towards the Buzzard |
 | Buzzard | Jumps to the 3rd square diagonally and from there can continue to slide orthogonally outward |
 | Camelrider | Repeatedly makes a (3,1) leap in the same direction |
 | Bent Shaman | It may: step 1 square; or jump 2 squares; or step 1 and jump 2 squares; or jump 2 squares then step 1 more square, always diagonally. It may change direction during its move |
 | Gingaroo | Makes a (4,1) leap, or jumps to the 2nd square diagonally |
 | Bishop | Slides diagonally |
 | Lynx | Makes a (3,2) leap, makes a Knight's jump, or slides orthogonally |
Rules
Pawns on the last rank can promote to Buzzard, Camelrider, Bent Shaman, Gingaroo, Bishop, or Lynx.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By HaruN Y.
Web page created: 2024-04-28. Web page last updated: 2024-04-28